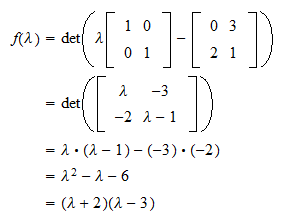Exemplary Tips About How To Check For Linear Independence

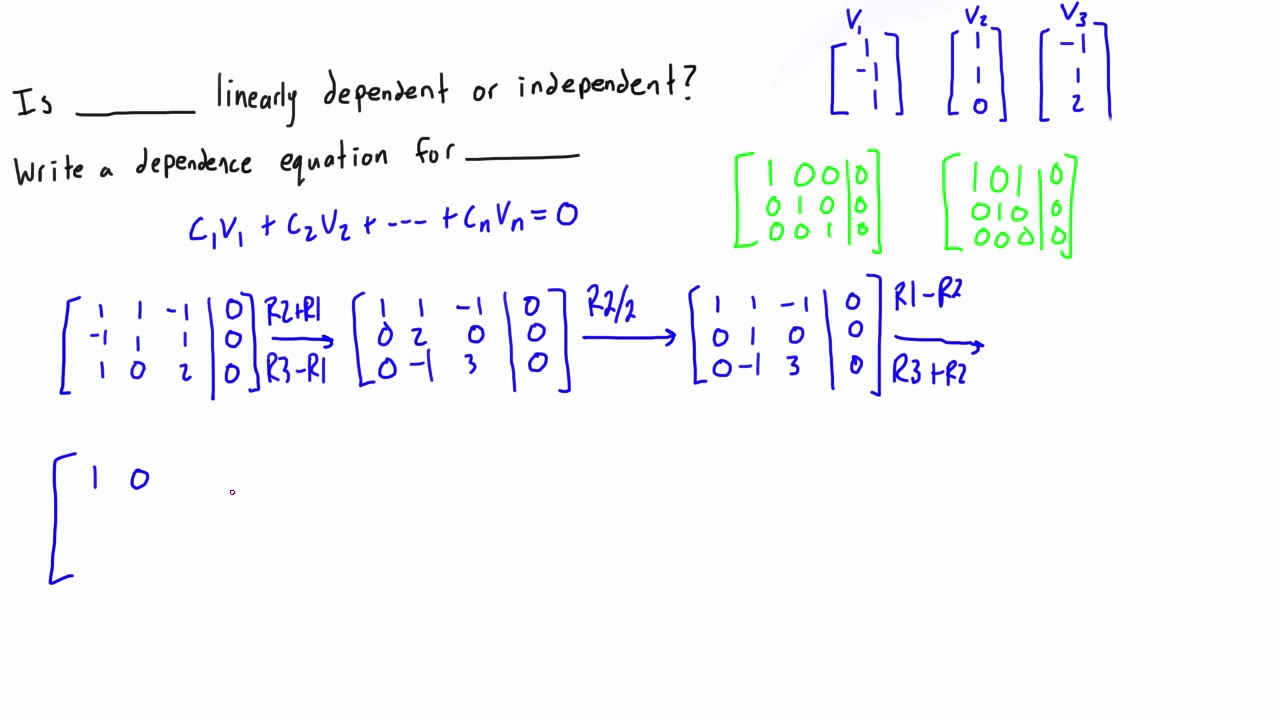
Check for linear independence 3 functions, using definition, 3 functions are linearly independent if c1f1+c2f2+c3f3=0 only has the solution that c1=c2=c3=0.

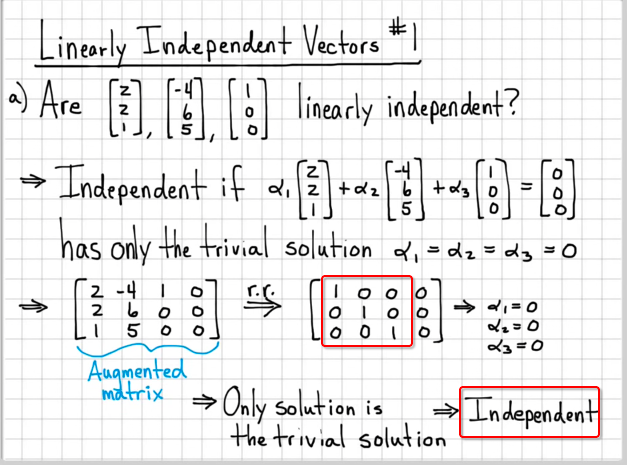
How to check for linear independence. Κ = λ m a x. | d | = 1 × | 1111 | − ( 1) × |. Has only the trivial solution.

If v1=cv2then v1−cv2=0,so {v1,v2}is linearly dependent. Results shows that x = [0; 0] inv (a) * b.

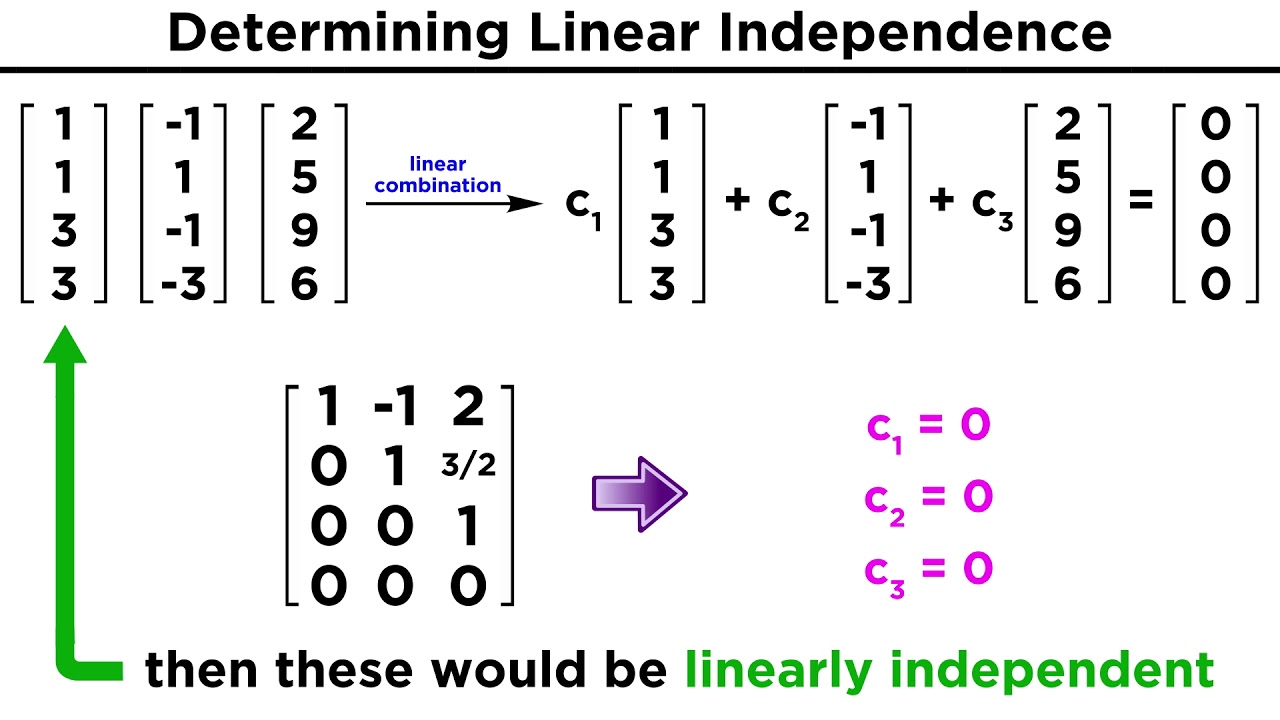
A determinant is a single number found from a matrix by multiplying and adding those numbers in a specific. It is easy to produce a linear dependence relation if one vector is. The test for linear independence uses matrix determinants.

In the other direction, if x1v1+x2v2=0with x1a=0(say), then v1=−x2x1v2. Is p(a) × p(b) = p(a and b)? The eigenvalues for this matrix are λ 1 = λ 2 = λ 3 = 0.001.

Isdependent = rank ( [s,v])==rank (s) jonas on 8 may 2021. |d|=0, then check for linear independence vectors a, b, c. 1 2] b = [0;

Check whether the vectors a = {1; How can we check whether two events are independent using probabilities? Finding the solution of the rref matrix.